Classification via Logistic Regression
As we gather
- Sit where ever you’d like
- Introduce yourself!
- Open today’s Rmd
- See Computational Intensity comparison
Announcements
- (Today) Thursday at 11:15am - MSCS Coffee Break
- Smail Gallery
- Share your thoughts about 1st floor OLRI hallway (e.g. furniture, whiteboards, etc)
- MSCS Logo contest!
- Due Feb 26 - see Slack for details
Where are we?
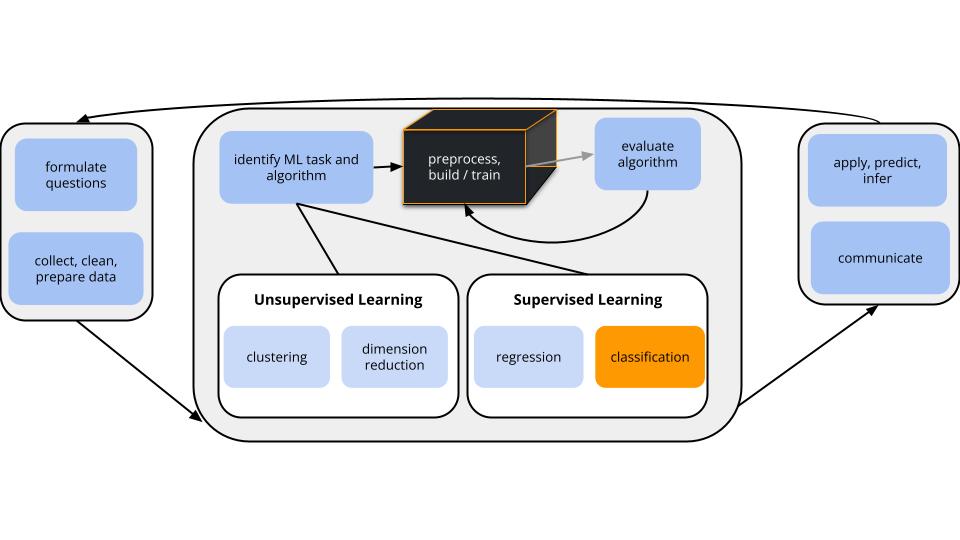
CONTEXT
world = supervised learning
We want to model some output variable \(y\) using a set of potential predictors \((x_1, x_2, ..., x_p)\).task = CLASSIFICATION
\(y\) is categorical and binary(parametric) algorithm
logistic regression
Notes: Logistic Regresison Review
Let \(y\) be a binary categorical response variable:
\[y = \begin{cases} 1 & \; \text{ if event happens} \\ 0 & \; \text{ if event doesn't happen} \\ \end{cases}\]Further define \[\begin{split} p &= \text{ probability event happens} \\ 1-p &= \text{ probability event doesn't happen} \\ \text{odds} & = \text{ odds event happens} = \frac{p}{1-p} \\ \end{split}\]
Then a logistic regression model of \(y\) by \(x\) is \[\begin{split} \log(\text{odds}) & = \beta_0 + \beta_1 x \\ \text{odds} & = e^{\beta_0 + \beta_1 x} \\ p & = \frac{\text{odds}}{\text{odds}+1} = \frac{e^{\beta_0 + \beta_1 x}}{e^{\beta_0 + \beta_1 x}+1} \\ \end{split}\]
Coefficient interpretation
\[\begin{split} \beta_0 & = \text{ LOG(ODDS) when } x=0 \\ e^{\beta_0} & = \text{ ODDS when } x=0 \\ \beta_1 & = \text{ unit change in LOG(ODDS) per 1 unit increase in } x \\ e^{\beta_1} & = \text{ multiplicative change in ODDS per 1 unit increase in } x \\ \end{split}\]
Example 1
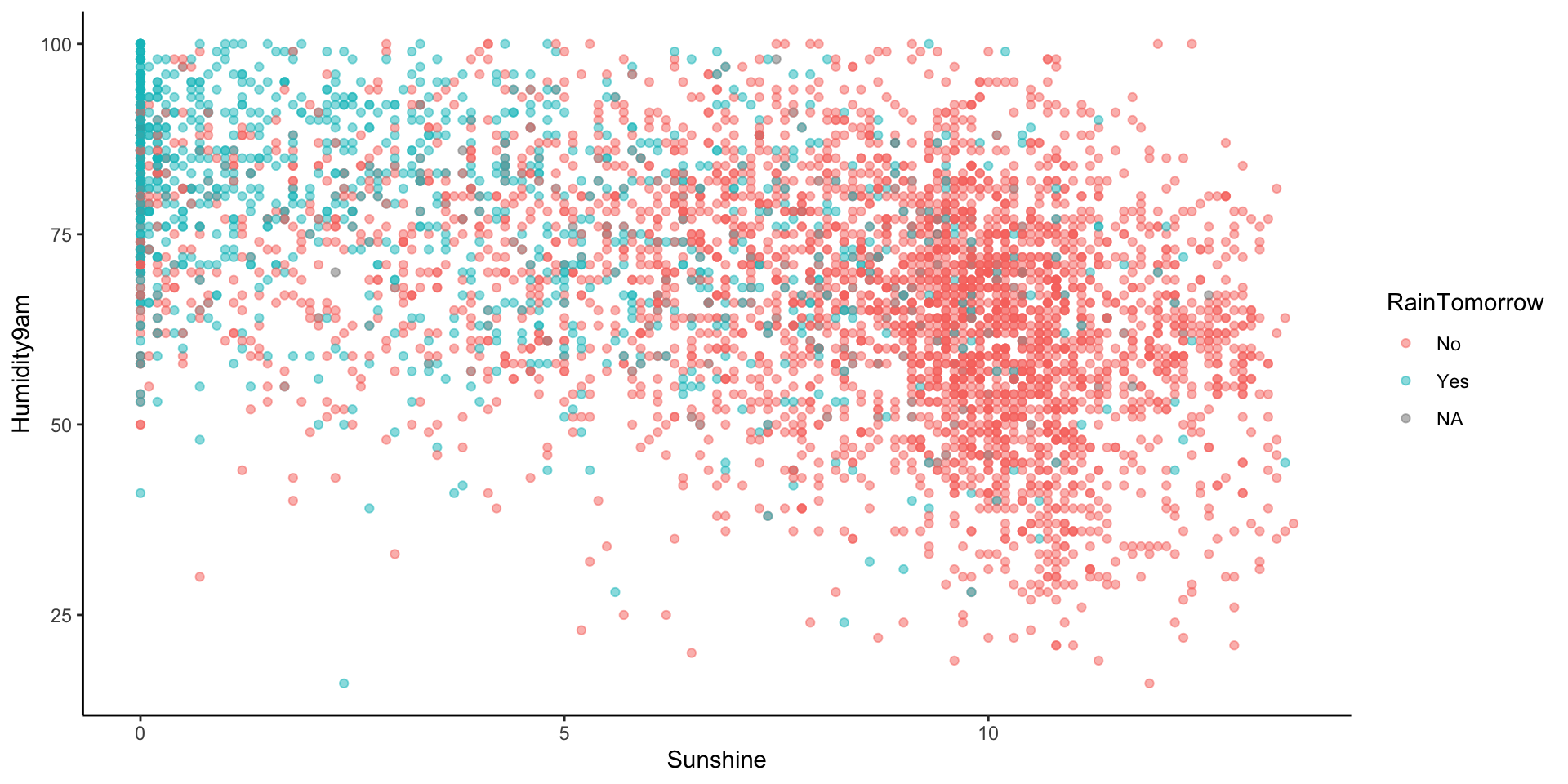
Let’s model RainTomorrow, whether or not it rains tomorrow in Sydney, by two predictors:
Humidity9am(% humidity at 9am today)Sunshine(number of hours of bright sunshine today)
Check out & comment on the relationship of rain with these 2 predictors:
Example 2
The logistic regression model is:
- log(odds of rain) = -1.01 + 0.0260 Humidity9am - 0.313 Sunshine
- odds of rain = exp(-1.01 + 0.0260 Humidity9am - 0.313 Sunshine)
- probability of rain = odds / (odds + 1)
Let’s interpret the Sunshine coefficient of -0.313:
- When controlling for humidity, and for every extra hour of sunshine, the LOG(ODDS) of rain…
- decrease by 0.313
- are roughly 31% as big (i.e. decrease by 69%)
- are roughly 73% as big (i.e. decrease by 27%)
- increase by 0.731
- When controlling for humidity, and for every extra hour of sunshine, the ODDS of rain…
- decrease by 0.313
- are roughly 31% as big (i.e. decrease by 69%)
- are roughly 73% as big (i.e. decrease by 27%)
- increase by 0.731
Example 2
The logistic regression model is:
- log(odds of rain) = -1.01 + 0.0260 Humidity9am - 0.313 Sunshine
- odds of rain = exp(-1.01 + 0.0260 Humidity9am - 0.313 Sunshine)
- probability of rain = odds / (odds + 1)
Let’s interpret the Sunshine coefficient of -0.313:
- When controlling for humidity, and for every extra hour of sunshine, the LOG(ODDS) of rain…
- decrease by 0.313
- When controlling for humidity, and for every extra hour of sunshine, the ODDS of rain…
- are roughly 73% as big (i.e. decrease by 27%)
Example 3
log(odds of rain) = -1.01 + 0.0260 Humidity9am - 0.313 Sunshine
Suppose there’s 99% humidity at 9am today and only 2 hours of bright sunshine.
- What’s the probability of rain?
Example 4
We used a simple classification rule above with a probability threshold of c = 0.5:
- If the probability of rain >= c, then predict rain.
- Otherwise, predict no rain.
Let’s translate this into a classification rule that partitions the data points into rain / no rain predictions based on the predictor values.
What do you think this classification rule / partition will look like?
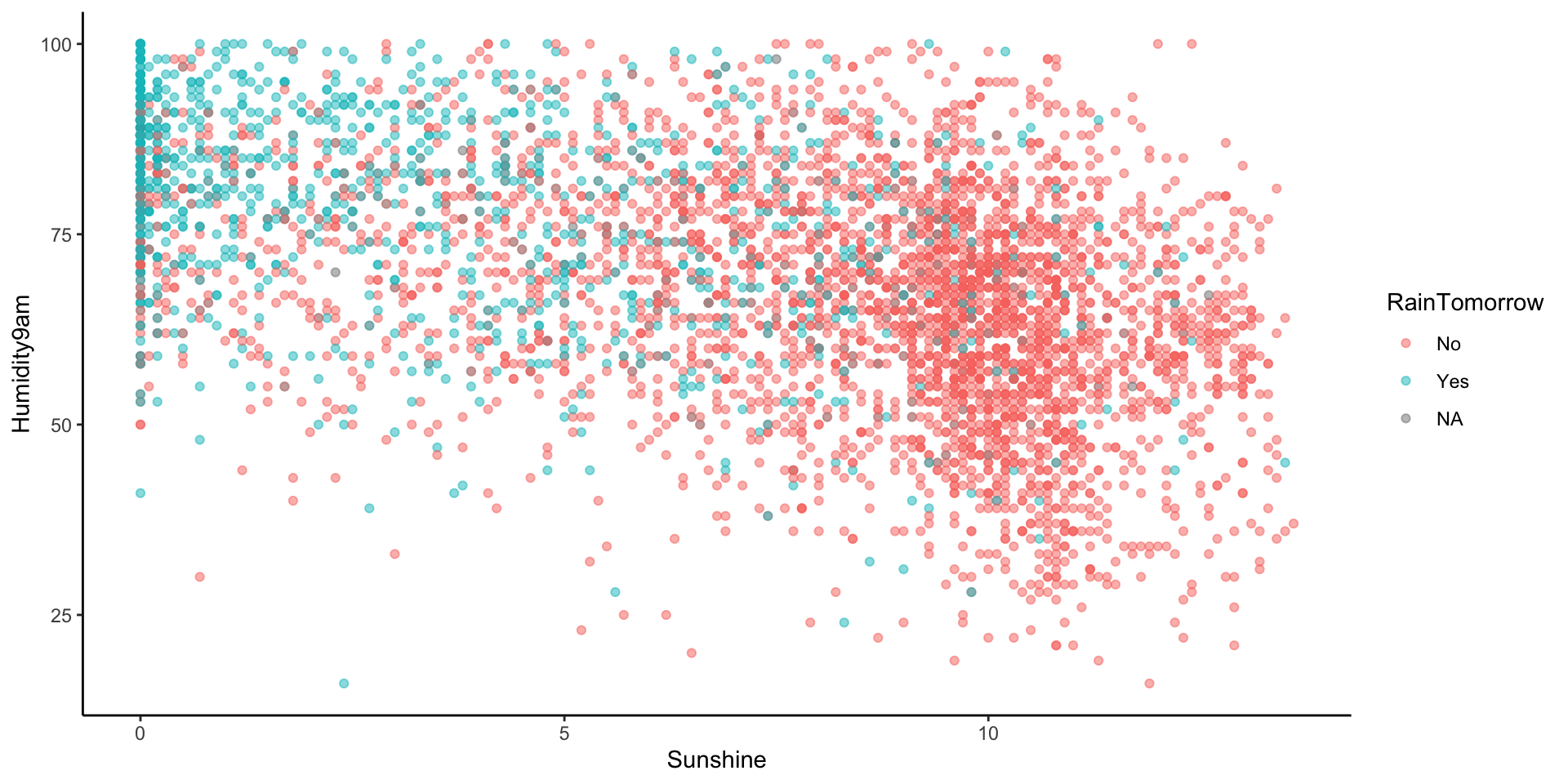
Example 5
- If …, then predict rain.
- Otherwise, predict no rain.
Work
Identify the pairs of humidity and sunshine values for which the probability of rain is 0.5, hence the log(odds of rain) is 0.
Set the log odds to 0:
log(odds of rain) = -1.01 + 0.0260 Humidity9am - 0.313 Sunshine = 0Solve for Humidity9am:
Move constant and Sunshine term to other side.
0.0260 Humidity9am = 1.01 + 0.3130 SunshineDivide both sides by 0.026:
Humidity9am = (1.01 / 0.026) + (0.3130 / 0.026) SunshineHumidity9am = 38.846 + 12.038 Sunshine
Example 6
Let’s visualize the partition, hence classification regions defined by our classification rule:
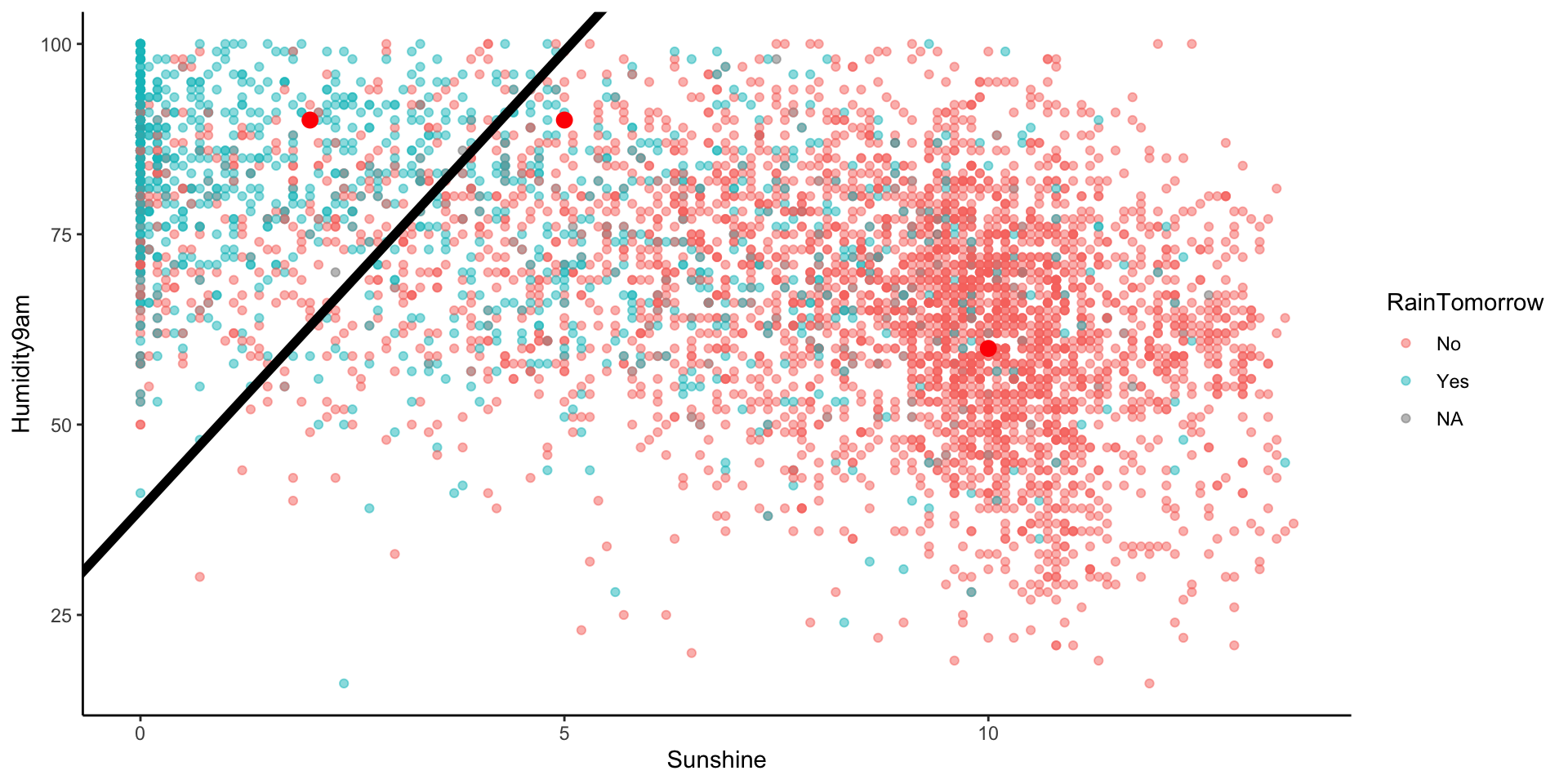
Use our classification rule to predict rain / no rain for the following days:
- Day 1: humidity = 90, sunshine = 2
- Day 2: humidity = 90, sunshine = 5
- Day 3: humidity = 60, sunshine = 10
Example 7
- Does the logistic regression algorithm have a tuning parameter?
No
- Estimating the logistic regression model requires the same pre-processing steps as least squares regression.
- Is it necessary to standardize quantitative predictors? If so, does the R function do this for us?
- Is it necessary to create dummy variables for our categorical predictors? If so, does the R function do this for us?
- No, R doesn’t standardize for logistic.
- Yes and Yes, R does this for us.
Small Group Activity
Work on exercises 1-8 [optional 9-10] with your group.
- Pay attention to new terms and concepts
After Class
Reflection & Review
- Use Concept Map to help you with HW4 and synthesis for Concept Quiz 1.
Group Assignment
- Make progress on finalizing the model your group is building.
Upcoming due dates
- Today: HW 4 (posted on Moodle)
- Tuesday Feb 27: Concept Quiz 1 on Units 1–3 (up to and including today)
- Work on Concept Map as a way to review & synthesize
- Tuesday Mar 5: Group Assignment 1
- Step 1: Submit brief report.
- Step 2: Submit test MAE.