7 AR and MA Models

Learning Goals

  • Understand the derivations of variance and covariance for the AR(1) and MA(1) model.
  • Understand the notation for an AR(p) and MA(q) models and the general mathematical approaches for deriving variance, covariance, and correlation.
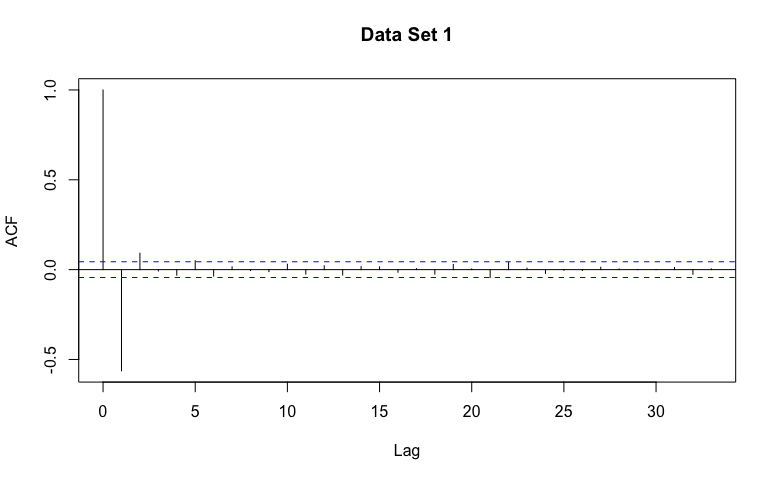
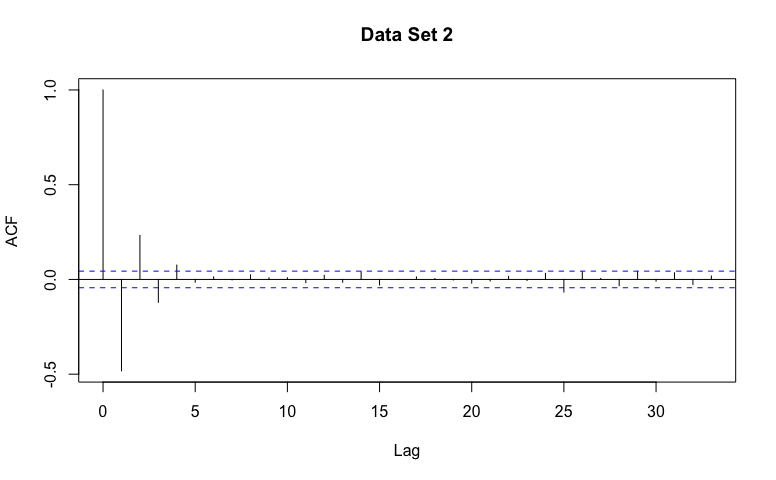
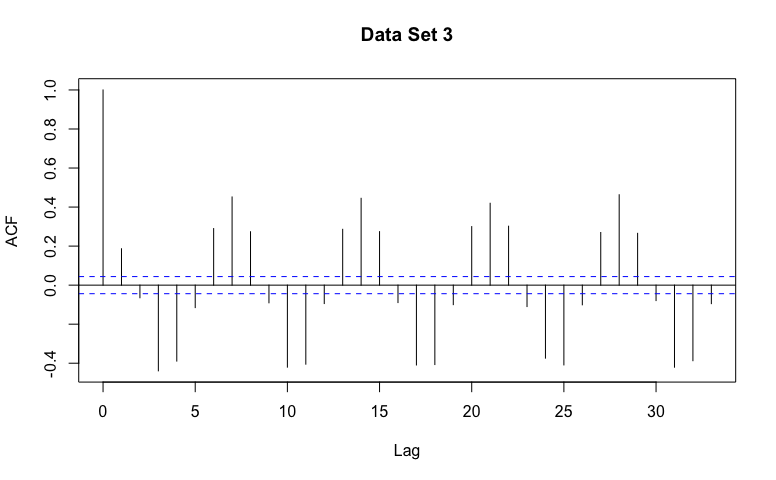
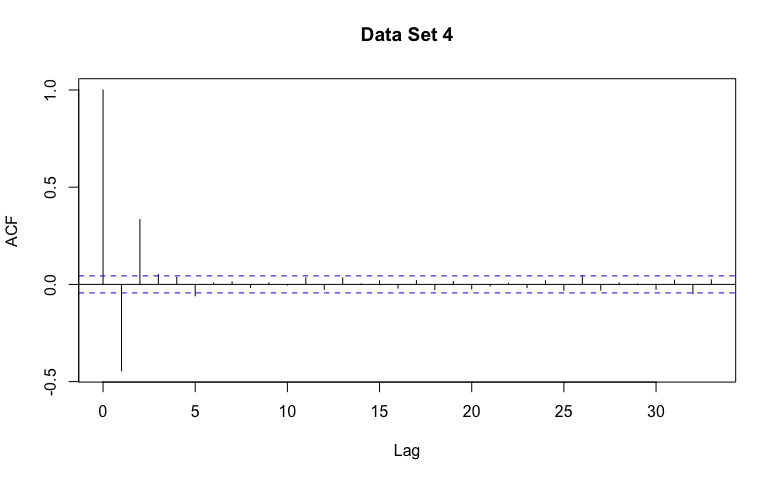
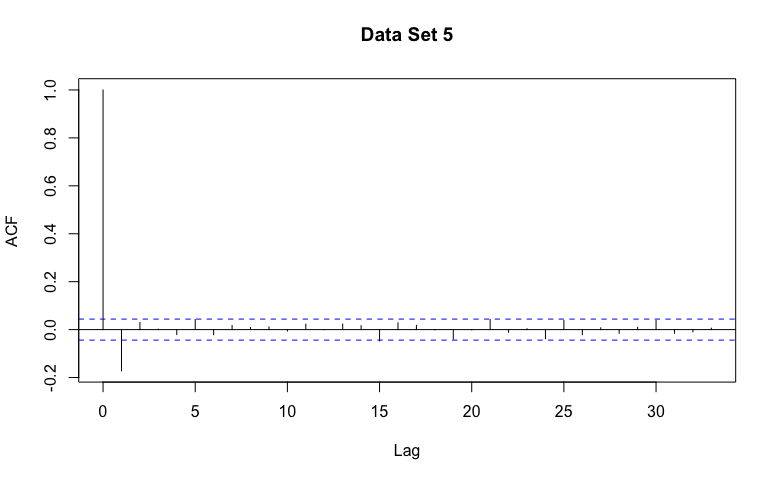
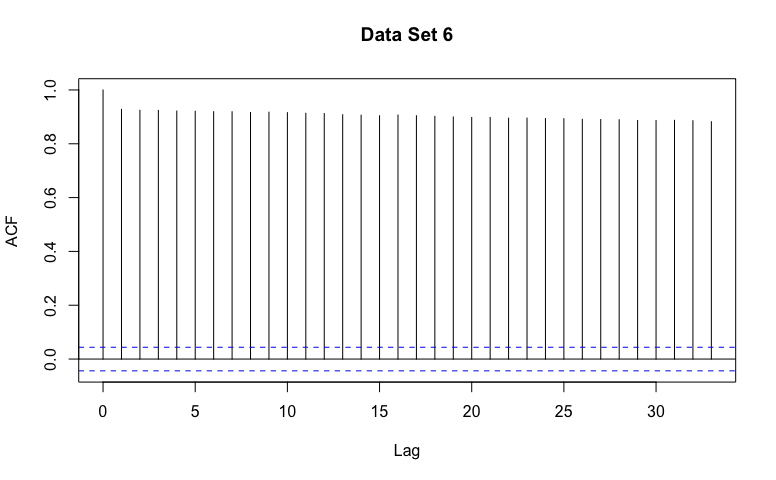
  • Recognize general patterns of non-stationarity, AR(p) models, and MA(q) models in example ACF graphs.

Class Warm Up

We’ll walk through the derivations for the MA(1) model as a class to warm up.

MA(1)

The MA(1) Model is

\[Y_t = W_t + \theta_1W_{t-1}\quad\text{ where }W_{t}\stackrel{iid}{\sim} N(0,\sigma^2_w), |\theta_1|<1\]

  1. Find the Expected value of \(Y_t\).

  2. Find the Variance of \(Y_t\).

  3. Find the Covariance of \(Y_t\) and \(Y_{t-h}\).

Group Theory

Working at the board, work through an alternative derivation for the AR(1) model.

Explicitly discuss with your partner how you’d like to collaborate today. It is your responsibility to make sure both you and your partner understand the derivation and that you are positively supporting each other in the process.

AR(1)

  1. Write down the model for an AR(1) Model.

\[Y_t = \]

  1. Rewrite the model by iteratively plugging in the value from the model for \(Y_{t-1}\) and then \(Y_{t-2}\). Keep going, to write \(Y_{t}\) as \(\sum^{\infty}_{k=0} \phi_1^k W_{t-k}\) allowing the time indices to range from \(-\infty,...,-3,-2,-1,0,1,2,3,...,\infty\)

For 7-8, use the infinite geometric series, \(\sum^{\infty}_{k=0} r^k = (1-r)^{-1}\text{ if }|r|<1\).

  1. Find the Expected value of \(Y_t\).

  2. Find the Variance of \(Y_t\).

  3. Find the Covariance of \(Y_t\) and \(Y_{t-h}\).

Name that Model

You’ve been selected to participate in our game show called, NAME that MODEL!

For each data set, guess AR, MA, or Not Stationary!

It may be useful to describe the general patterns you might expect in the estimated ACF for data generated from an AR, MA, or Not Stationary model.

Data set 1

Data set 2

Data set 3

Data set 4

Data set 5

Data set 6