7.1 Coordinate Reference Systems (CRS)
At the heart of every spatial visualization is a set of locations. One way to describe a location is in terms of coordinates and a coordinate reference system (known as CRS).
There are three main components to a CRS: ellipsoid, datum, and a projection.
7.1.1 Ellipsoid
While you might have learned that the Earth is a sphere, it is actually closer to an ellipsoid with a bulge at the equator. Additionally, the surface is irregular and not smooth. To define a CRS, we first need to choose a mathematical model represent a smooth approximation to the shape of the Earth. The common ellipsoid models are known as WGS84 and GRS80. See the illustration below of one ellipsoid model (shown in black) as compared to Earth’s true irregular surface (shown in red).
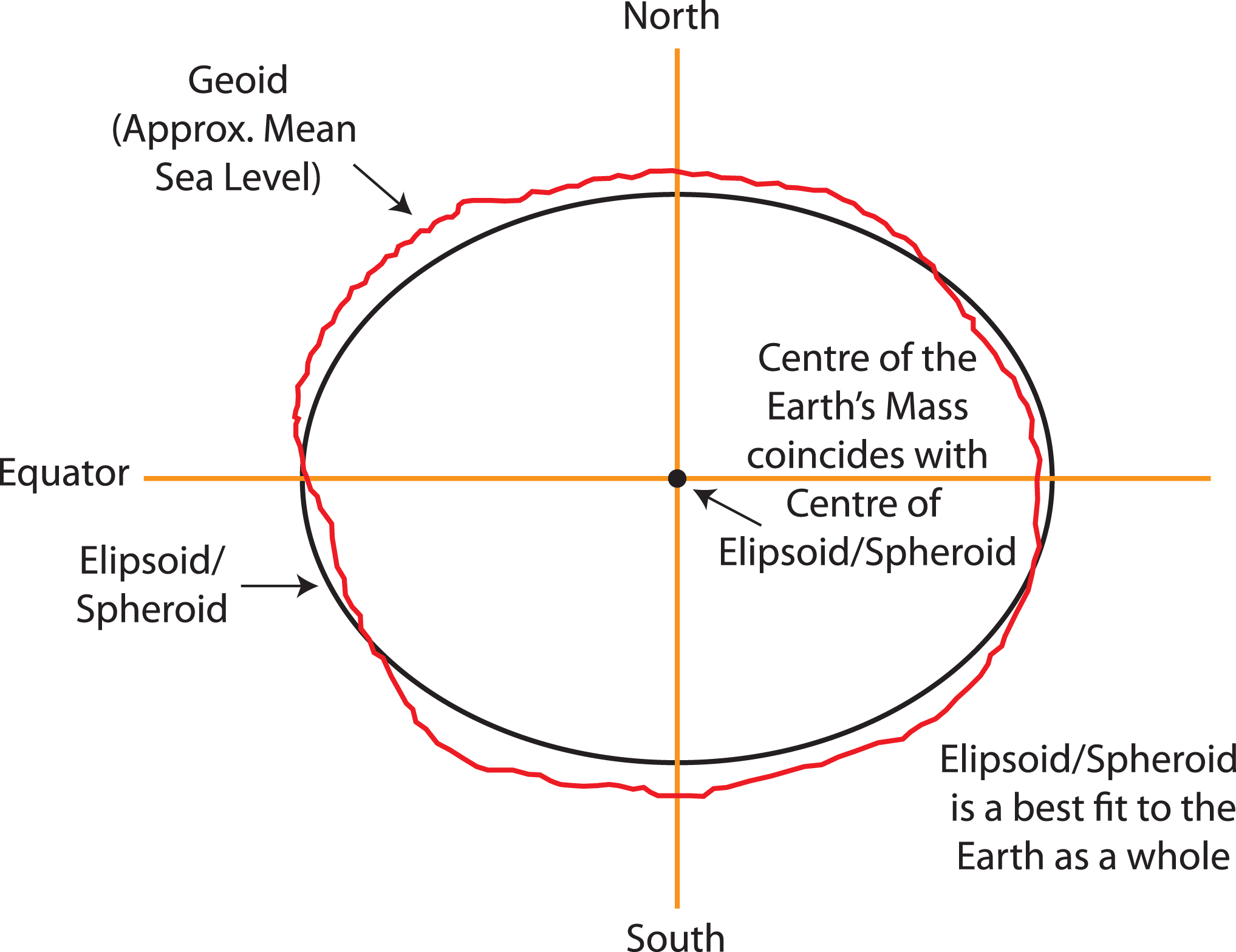
7.1.2 Datum
Each ellipsoid model has different ways to position it self relative to Earth depending on the center or origin. Each potential position and reference frame for representing the position of locations on Earth is called a datum.
For example, two different datum for the same ellipsoid model can provide a more accurate fit or approximation of the Earth’s surface depending on the region of interest (South America v. North America). For example, the NAD83 datum is a good fit for the GRS80 ellipsoid in North America, but SIRGAS2000 is a better fit for the GRS80 ellipsoid in South America. The illustration below shows one datum in which the center of the ellipsoid does not coincide with the center of Earth’s mass. With this position of the ellipsoid, we gain a better fit for the southern half of the Earth.
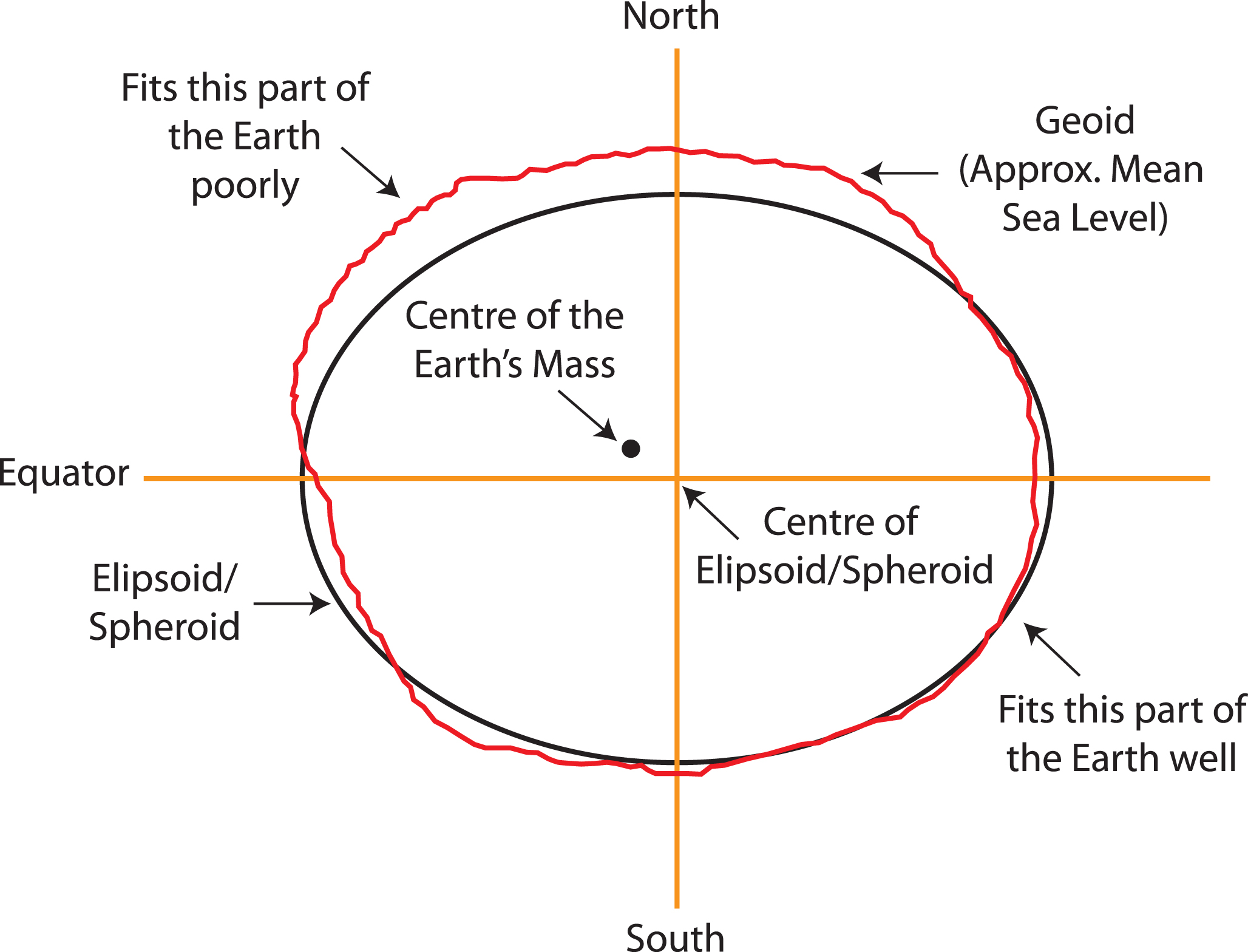
It is useful to know that the Global Positioning System (GPS) uses the WGS84 ellipsoid model and a datum by the same name, which provides an overall best fit of the Earth.
If you have longitude and latitude coordinates for a location, it is important to know what datum and ellipsoid were used to define those positions.
Note: In practice, the horizontal distance between WGS84 and NAD83 coordinates is about 3-4 feet in the US, which may not be significant for most applications.
The 3 most common datum/ellipsoids used in the U.S.:
WGS84 (EPSG: 4326)
+init=epsg:4326 +proj=longlat +ellps=WGS84
+datum=WGS84 +no_defs +towgs84=0,0,0
## CRS used by Google Earth and the U.S. Department of Defense for all their mapping.
## Tends to be used for global reference systems.
## GPS satellites broadcast the predicted WGS84 orbits.NAD83 (EPSG: 4269)
+init=epsg:4269 +proj=longlat +ellps=GRS80 +datum=NAD83
+no_defs +towgs84=0,0,0
##Most commonly used by U.S. federal agencies.
## Aligned with WGS84 at creation, but has since drifted.
## Although WGS84 and NAD83 are not equivalent, for most applications they are very similar.NAD27 (EPSG: 4267)
+init=epsg:4267 +proj=longlat +ellps=clrk66 +datum=NAD27
+no_defs
+nadgrids=@conus,@alaska,@ntv2_0.gsb,@ntv1_can.dat
## Has been replaced by NAD83, but is still encountered!For more resources related to EPSG, go to https://epsg.io/ and https://spatialreference.org/.
7.1.3 Projection
Lastly, we must project the 3D ellipse on a 2D surface to make a map with Easting and Northing coordinates. Flattening a round object without distortion is impossible, resulting in trade-offs between area, direction, shape, and distance. For example, distance and direction are trade-offs because both features can not be simultaneously preserved. No “best” projection exists, but some are better suited to different applications.
For a good overview of common projection methods, see https://pubs.usgs.gov/gip/70047422/report.pdf.
One of the most commonly used projection is the Mercator projection which is a cylindrical map projection from the 1500’s. It became popular for navigation because it represented north as up and south as down everywhere and preserves local directions and shape. However, it inflates the size of regions far from the equator. Thus, Greenland, Antarctica, Canada, and Russia appear large relative to their actual land mass as compared to Central Africa. See the illustration below to compare the area/shape of the countries with the Mercator projection of the world (light blue) with the true areas/shapes (dark blue).
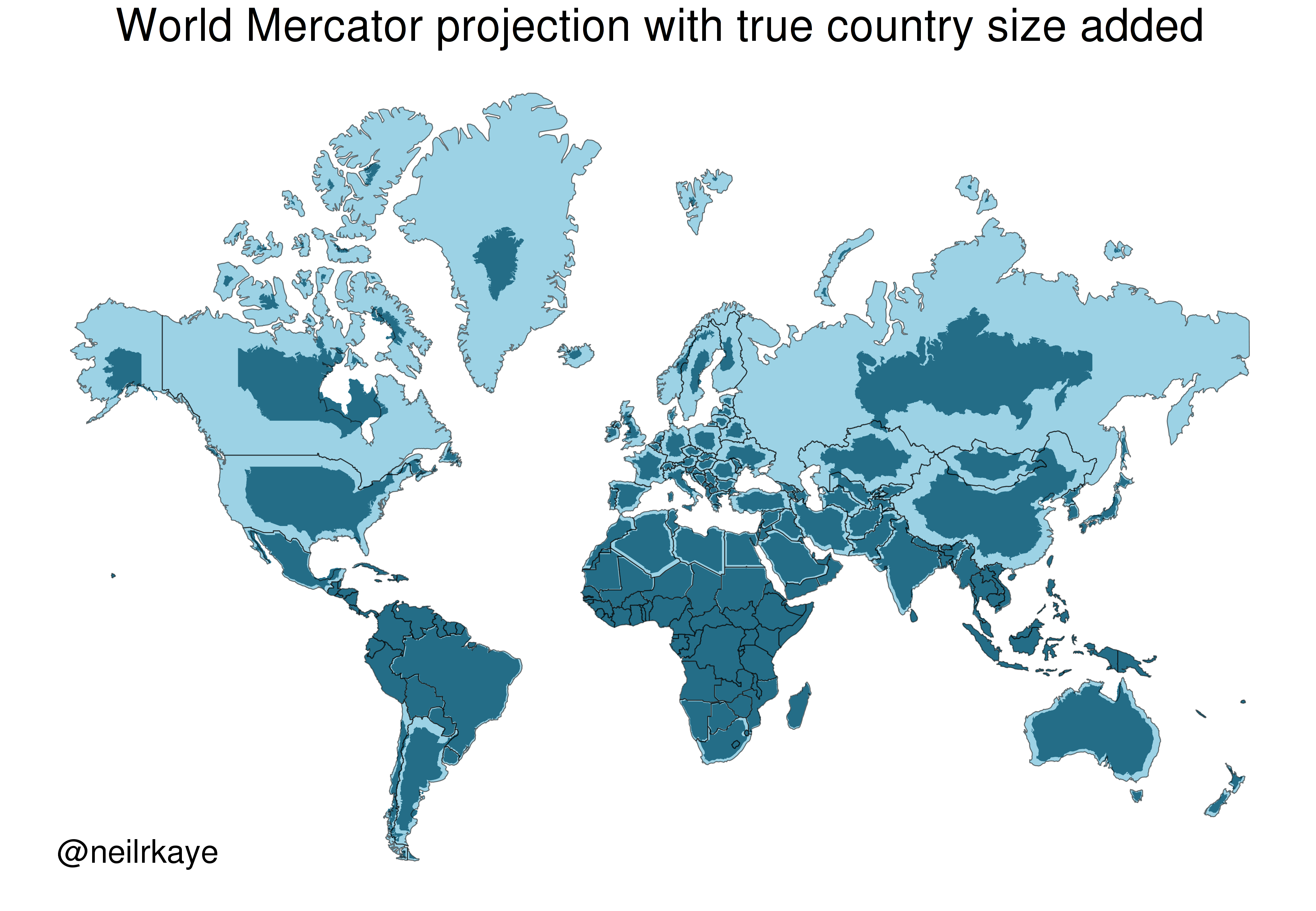
Below you can see four different world projections. Take note of what is lost in terms of angle, area, or distance in these projections.
library(rnaturalearth)
world <- ne_countries(scale = "medium", returnclass = "sf")
# Basic Map w/ labels
ggplot(data = world) +
geom_sf(color = "black", fill = "#bada55") +
labs(x = "Longitude", y = "Latitude", title = "World Map - Mercator Projection", subtitle = paste0("(", length(unique(world$name)), " countries)")) +
theme_bw()
ggplot(data = world) +
geom_sf(color = "black", fill = "#bada55") +
coord_sf(crs = "+proj=laea +lat_0=52 +lon_0=10 +x_0=4321000 +y_0=3210000 +ellps=GRS80 +units=m +no_defs") +
labs(title = "Lambert Azimuthal Equal-Area Projection", subtitle = "Correctly represents area but not angles") +
theme_bw()
ggplot(data = world) +
geom_sf(color = "black", fill = "#bada55") +
coord_sf(crs = "+proj=fouc") +
labs(title = "Foucaut Projection", subtitle = "Correctly represents area, lots of distortion in high latitudes") +
theme_bw()
ggplot(data = world) +
geom_sf(color = "black", fill = "#bada55") +
coord_sf(crs = "+proj=natearth2") +
labs(title = "Natural Earth II Projection", subtitle = "Represents globe shape, distorted at high latitudes") +
theme_bw() It is important to consider what ellipsoid, datum, and projection your locations have been recorded and mapped using.