5.10 Seasonal ARIMA Models
The s in the sarima() stands for seasonal. A Seasonal ARIMA model allows us to add a seasonal lag (e.g. 12) into an ARMA model. The model is written as
\[\Phi(B^S)\phi(B)Y_t = \Theta(B^S)\theta(B)W_t\] where the non-seasonal components are: \[\phi(B) =1 - \phi_1B- \phi_2B^2 - \cdots - \phi_pB^p\] and \[\theta(B) = 1+ \theta_1B+ \theta_2B^2 + \cdots + \theta_qB^q\] and the seasonal components are: \[\Phi(B^S) =1 - \Phi_1B^S- \Phi_2B^{2S} - \cdots - \Phi_pB^{PS}\] and \[\Theta(B^S) = 1+ \Theta_1B^S+ \Theta_2B^{2S} + \cdots + \Theta_qB^{QS}\]
Why might you need a Seasonal ARMA?
If you see strong seasonal autocorrelation in the residuals after you fit a good ARMA model, try a seasonal ARMA.
If there is strong seasonal autocorrelation (non-zero values at lag \(S\), \(2S\), etc.) that drops off after Q seasonal lags, you can fit a seasonal MA(Q) model.
On the other hand if you see a strong seasonal partial autocorrelation that drops off after P seasonal lags, you can fit a seasonal AR(P) model.
acf2(resid(GoodMod$fit)) #Notice the high ACF and PACF for lag 1 year (12 months) -- only look at 1 year, 2 year, etc. is there a pattern?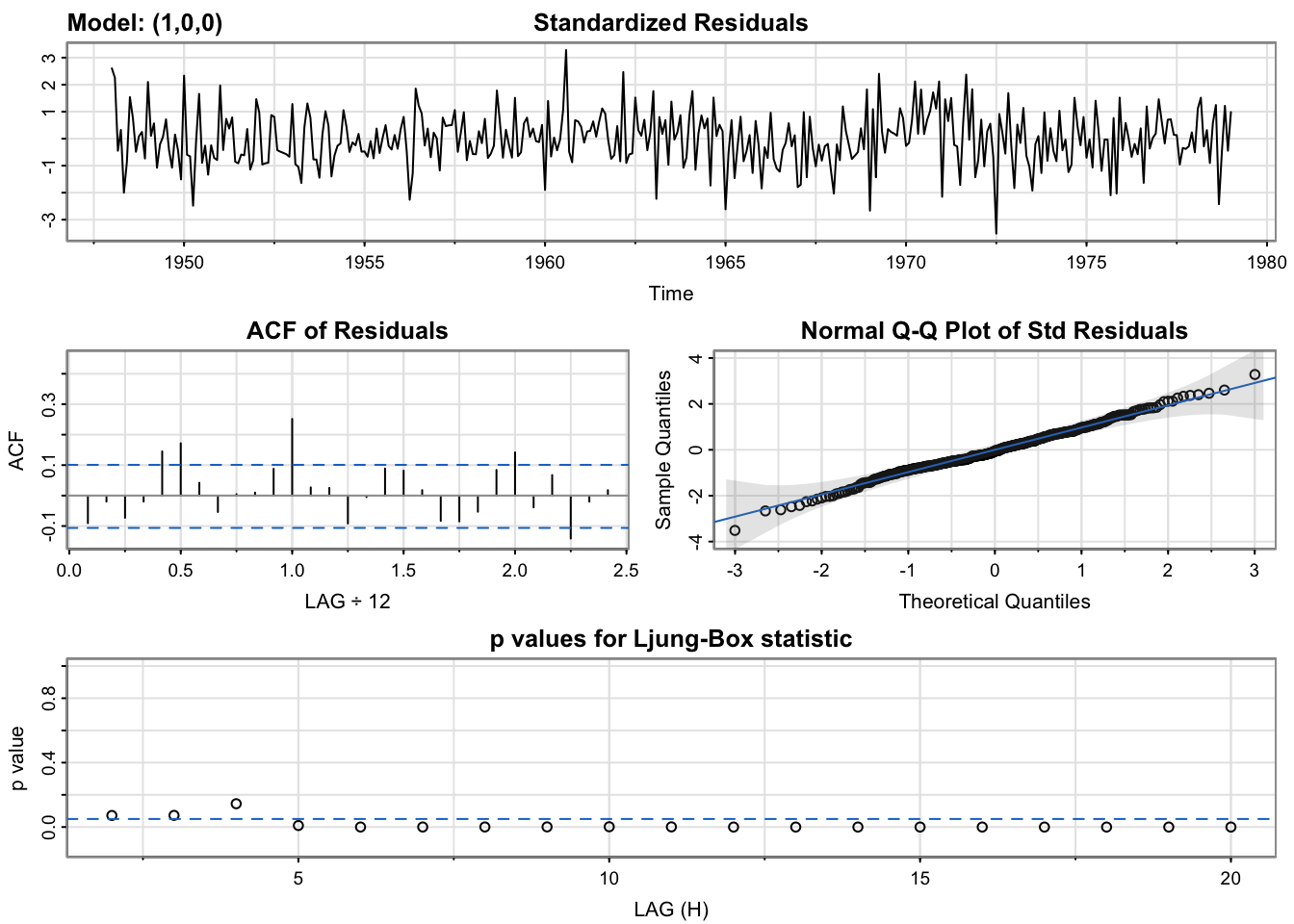
## [,1] [,2] [,3] [,4] [,5] [,6]
## ACF 0.07 -0.12 -0.17 -0.07 0.10 0.08
## PACF 0.07 -0.13 -0.16 -0.06 0.07 0.03
## [,7] [,8] [,9] [,10] [,11] [,12]
## ACF -0.02 -0.09 -0.03 0.01 0.12 0.18
## PACF -0.03 -0.05 0.00 -0.01 0.09 0.17
## [,13] [,14] [,15] [,16] [,17] [,18]
## ACF 0.06 -0.01 -0.08 -0.02 0.07 0.04
## PACF 0.09 0.07 -0.01 0.02 0.05 0.01
## [,19] [,20] [,21] [,22] [,23] [,24]
## ACF 0.00 -0.08 -0.10 -0.01 0.14 0.11
## PACF 0.02 -0.04 -0.08 -0.04 0.06 0.03
## [,25] [,26] [,27] [,28] [,29] [,30]
## ACF 0.05 0.09 -0.07 -0.03 -0.02 -0.04
## PACF 0.04 0.15 -0.02 -0.01 -0.03 -0.06
## [,31] [,32] [,33] [,34] [,35] [,36]
## ACF 0.00 0.06 -0.11 -0.06 0.05 0.08
## PACF -0.02 0.09 -0.10 -0.06 -0.01 -0.01
## [,37] [,38] [,39] [,40] [,41] [,42]
## ACF 0.15 -0.06 -0.07 -0.04 0.04 0.09
## PACF 0.08 -0.08 0.01 -0.02 0.03 0.06
## [,43] [,44] [,45] [,46] [,47] [,48]
## ACF -0.02 -0.11 -0.12 0.08 0.10 0.08
## PACF -0.03 -0.05 -0.05 0.10 0.06 0.02mod.fit5 <- sarima(birthTS$Value, p = 1,d = 0, q = 1,P = 0, D = 0, Q = 1, S = 12, xreg = X) #ARMA(1,1) + SeasonalMA(1)## initial value 2.384529
## iter 2 value 2.147927
## iter 3 value 2.136802
## iter 4 value 1.945477
## iter 5 value 1.926679
## iter 6 value 1.907587
## iter 7 value 1.904334
## iter 8 value 1.901634
## iter 9 value 1.901307
## iter 10 value 1.901008
## iter 11 value 1.900730
## iter 12 value 1.900127
## iter 13 value 1.899728
## iter 14 value 1.899543
## iter 15 value 1.899475
## iter 16 value 1.899416
## iter 17 value 1.899381
## iter 18 value 1.899359
## iter 19 value 1.899336
## iter 20 value 1.899302
## iter 21 value 1.899264
## iter 22 value 1.899242
## iter 23 value 1.899237
## iter 24 value 1.899236
## iter 25 value 1.899236
## iter 26 value 1.899236
## iter 27 value 1.899235
## iter 28 value 1.899234
## iter 29 value 1.899233
## iter 30 value 1.899233
## iter 31 value 1.899233
## iter 31 value 1.899233
## iter 31 value 1.899233
## final value 1.899233
## converged
## initial value 1.909564
## iter 2 value 1.908813
## iter 3 value 1.908494
## iter 4 value 1.907321
## iter 5 value 1.905983
## iter 6 value 1.904699
## iter 7 value 1.903991
## iter 8 value 1.903586
## iter 9 value 1.903277
## iter 10 value 1.903073
## iter 11 value 1.902929
## iter 12 value 1.902760
## iter 13 value 1.902454
## iter 14 value 1.901742
## iter 15 value 1.901352
## iter 16 value 1.900946
## iter 17 value 1.900397
## iter 18 value 1.899980
## iter 19 value 1.899814
## iter 20 value 1.899592
## iter 21 value 1.899478
## iter 22 value 1.899358
## iter 23 value 1.899262
## iter 24 value 1.899108
## iter 25 value 1.898971
## iter 26 value 1.898827
## iter 27 value 1.898691
## iter 28 value 1.898580
## iter 29 value 1.898430
## iter 30 value 1.898332
## iter 31 value 1.898269
## iter 32 value 1.898205
## iter 33 value 1.898067
## iter 34 value 1.897778
## iter 35 value 1.897284
## iter 36 value 1.896761
## iter 37 value 1.896542
## iter 38 value 1.896514
## iter 39 value 1.896509
## iter 40 value 1.896504
## iter 41 value 1.896500
## iter 42 value 1.896491
## iter 43 value 1.896475
## iter 44 value 1.896436
## iter 45 value 1.896366
## iter 46 value 1.896269
## iter 47 value 1.896191
## iter 48 value 1.896156
## iter 49 value 1.896143
## iter 50 value 1.896136
## iter 51 value 1.896126
## iter 52 value 1.896112
## iter 53 value 1.896093
## iter 54 value 1.896071
## iter 55 value 1.896056
## iter 56 value 1.896050
## iter 57 value 1.896046
## iter 58 value 1.896039
## iter 59 value 1.896022
## iter 60 value 1.895983
## iter 61 value 1.895918
## iter 62 value 1.895850
## iter 63 value 1.895813
## iter 64 value 1.895805
## iter 65 value 1.895804
## iter 66 value 1.895801
## iter 67 value 1.895796
## iter 68 value 1.895788
## iter 69 value 1.895782
## iter 70 value 1.895779
## iter 71 value 1.895779
## iter 72 value 1.895778
## iter 73 value 1.895777
## iter 74 value 1.895774
## iter 75 value 1.895766
## iter 76 value 1.895750
## iter 77 value 1.895729
## iter 78 value 1.895714
## iter 79 value 1.895710
## iter 80 value 1.895710
## iter 81 value 1.895710
## iter 82 value 1.895710
## iter 83 value 1.895710
## iter 84 value 1.895710
## iter 85 value 1.895709
## iter 86 value 1.895709
## iter 87 value 1.895709
## iter 88 value 1.895709
## iter 89 value 1.895709
## iter 90 value 1.895709
## iter 91 value 1.895709
## iter 92 value 1.895708
## iter 93 value 1.895708
## iter 94 value 1.895707
## iter 95 value 1.895706
## iter 96 value 1.895705
## iter 97 value 1.895705
## iter 98 value 1.895705
## iter 99 value 1.895705
## iter 100 value 1.895705
## final value 1.895705
## stopped after 100 iterations## Warning in stats::arima(xdata, order
## = c(p, d, q), seasonal = list(order =
## c(P, : possible convergence problem:
## optim gave code = 1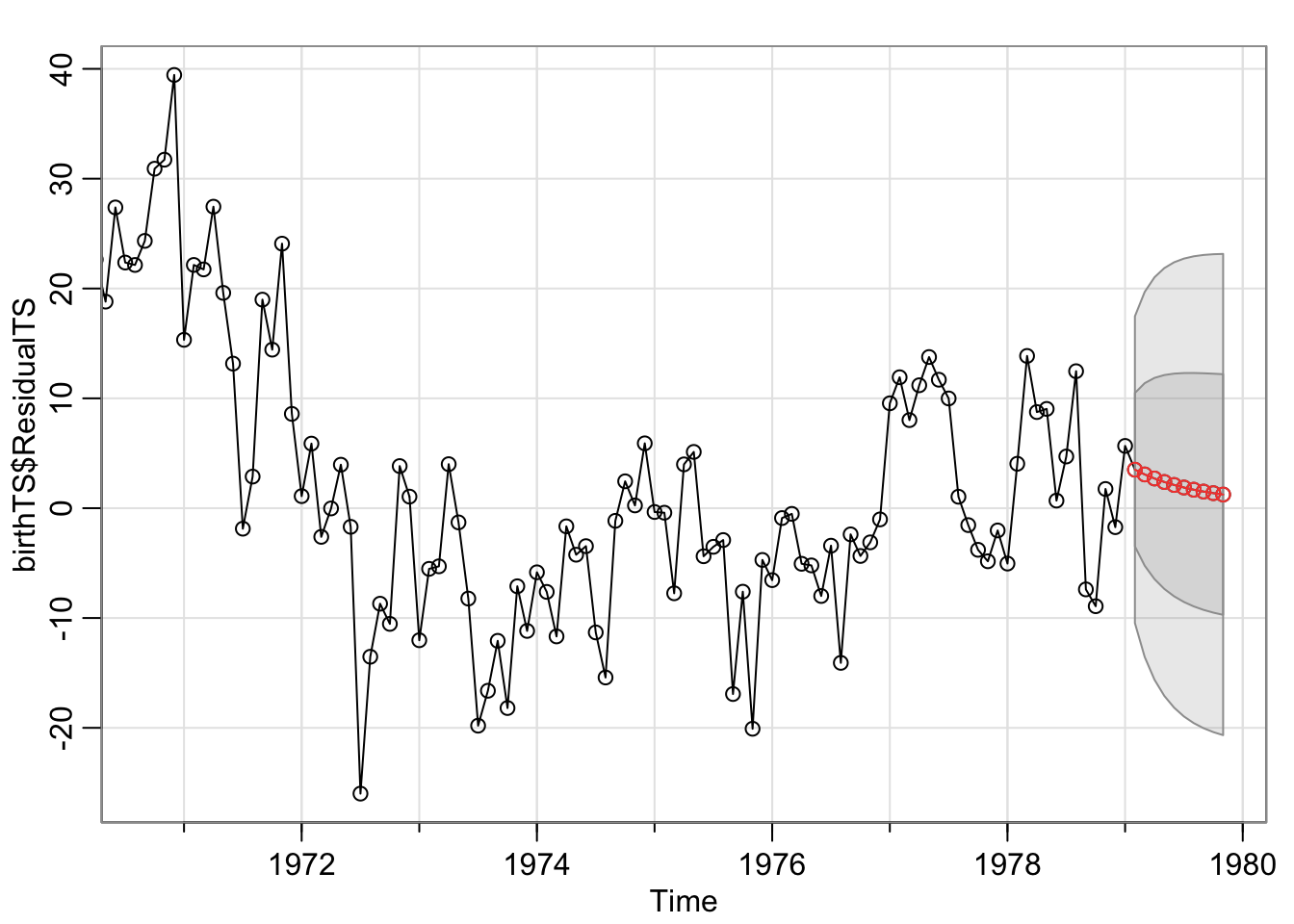
mod.fit5$BIC## [1] 6.95mod.fit6 <- sarima(birthTS$Value, p = 1,d = 0, q = 1,P = 1, D = 0, Q = 0, S = 12, xreg = X) #ARMA(1,1) + SeasonalAR(1)## initial value 2.362596
## iter 2 value 2.120951
## iter 3 value 2.072454
## iter 4 value 1.923888
## iter 5 value 1.906932
## iter 6 value 1.886497
## iter 7 value 1.882961
## iter 8 value 1.880919
## iter 9 value 1.880627
## iter 10 value 1.880389
## iter 11 value 1.880105
## iter 12 value 1.879532
## iter 13 value 1.879173
## iter 14 value 1.879013
## iter 15 value 1.878944
## iter 16 value 1.878887
## iter 17 value 1.878849
## iter 18 value 1.878821
## iter 19 value 1.878796
## iter 20 value 1.878765
## iter 21 value 1.878723
## iter 22 value 1.878685
## iter 23 value 1.878669
## iter 24 value 1.878666
## iter 25 value 1.878666
## iter 26 value 1.878665
## iter 27 value 1.878665
## iter 28 value 1.878664
## iter 29 value 1.878664
## iter 30 value 1.878663
## iter 31 value 1.878663
## iter 32 value 1.878663
## iter 33 value 1.878663
## iter 34 value 1.878662
## iter 35 value 1.878662
## iter 36 value 1.878662
## iter 37 value 1.878661
## iter 38 value 1.878661
## iter 39 value 1.878661
## iter 40 value 1.878661
## iter 41 value 1.878661
## iter 41 value 1.878661
## iter 41 value 1.878661
## final value 1.878661
## converged
## initial value 1.908939
## iter 2 value 1.906172
## iter 3 value 1.905234
## iter 4 value 1.904126
## iter 5 value 1.903103
## iter 6 value 1.901355
## iter 7 value 1.899815
## iter 8 value 1.898479
## iter 9 value 1.897673
## iter 10 value 1.897058
## iter 11 value 1.896601
## iter 12 value 1.896394
## iter 13 value 1.896286
## iter 14 value 1.896152
## iter 15 value 1.895954
## iter 16 value 1.895737
## iter 17 value 1.895578
## iter 18 value 1.895496
## iter 19 value 1.895422
## iter 20 value 1.895271
## iter 21 value 1.894916
## iter 22 value 1.894736
## iter 23 value 1.894619
## iter 24 value 1.894499
## iter 25 value 1.894462
## iter 26 value 1.894422
## iter 27 value 1.894356
## iter 28 value 1.894258
## iter 29 value 1.894177
## iter 30 value 1.894059
## iter 31 value 1.893961
## iter 32 value 1.893880
## iter 33 value 1.893745
## iter 34 value 1.893440
## iter 35 value 1.893012
## iter 36 value 1.892616
## iter 37 value 1.892274
## iter 38 value 1.892203
## iter 39 value 1.892186
## iter 40 value 1.892179
## iter 41 value 1.892177
## iter 42 value 1.892171
## iter 43 value 1.892160
## iter 44 value 1.892136
## iter 45 value 1.892097
## iter 46 value 1.892052
## iter 47 value 1.892024
## iter 48 value 1.892015
## iter 49 value 1.892009
## iter 50 value 1.891998
## iter 51 value 1.891985
## iter 52 value 1.891969
## iter 53 value 1.891956
## iter 54 value 1.891948
## iter 55 value 1.891944
## iter 56 value 1.891943
## iter 57 value 1.891941
## iter 58 value 1.891938
## iter 59 value 1.891932
## iter 60 value 1.891921
## iter 61 value 1.891905
## iter 62 value 1.891894
## iter 63 value 1.891890
## iter 64 value 1.891888
## iter 65 value 1.891885
## iter 66 value 1.891879
## iter 67 value 1.891868
## iter 68 value 1.891854
## iter 69 value 1.891845
## iter 70 value 1.891843
## iter 71 value 1.891843
## iter 72 value 1.891843
## iter 73 value 1.891843
## iter 74 value 1.891842
## iter 75 value 1.891839
## iter 76 value 1.891835
## iter 77 value 1.891826
## iter 78 value 1.891816
## iter 79 value 1.891811
## iter 80 value 1.891810
## iter 81 value 1.891810
## iter 82 value 1.891810
## iter 83 value 1.891810
## iter 84 value 1.891810
## iter 85 value 1.891810
## iter 86 value 1.891809
## iter 87 value 1.891809
## iter 87 value 1.891809
## iter 87 value 1.891809
## final value 1.891809
## converged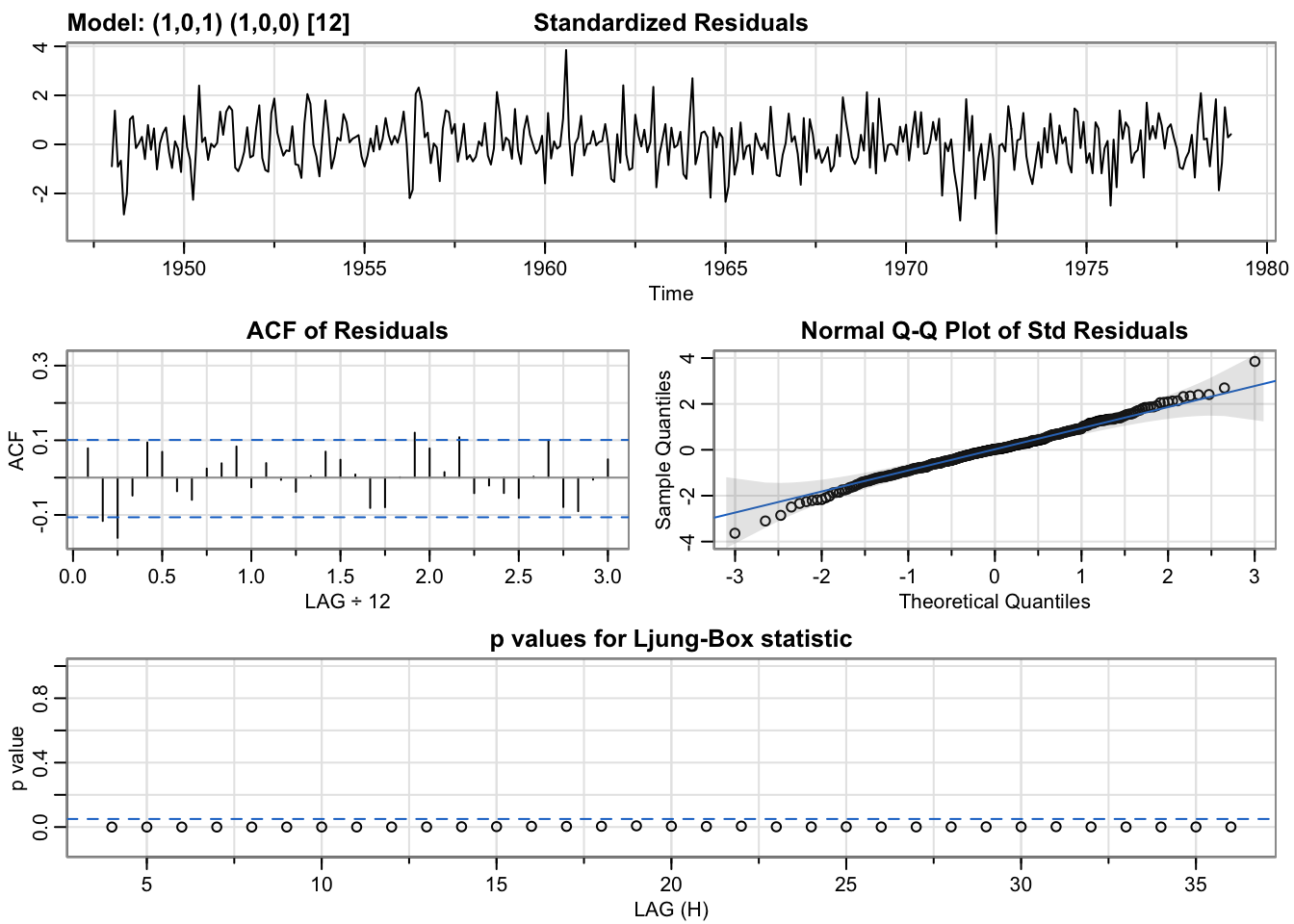
mod.fit6$BIC## [1] 6.94GoodMod$BIC## [1] 6.96While the p-values are still not ideal, the model with spline trend, indicator variables for month, ARMA(1,1) + SeasonalAR(1) for errors has the lowest BIC and the SARIMA coefficients are all significantly different from zero.