9  ARIMA and SARIMA Models

Settling In

  • Check Slack for Announcements!
  • Content Conversation 1
    • During class time on Thursday (in classroom)
    • Be prepared to walk through \(Cor(Y_t,Y_{t-h})\) derivation for \(MA(q)\) on the whiteboard.
  • Homework 4
    • Everyone can have until tonight at midnight to submit HW4 (no extra grace period).
    • I’ll be giving feedback for you to incorporate into Mini Project 1
  • Mini Project 1
    • Due next Tuesday

Everything on the slides is in the online manual: https://bcheggeseth.github.io/452_fall_2025/

Highlights from Day 8

Model Selection for ARMA Models

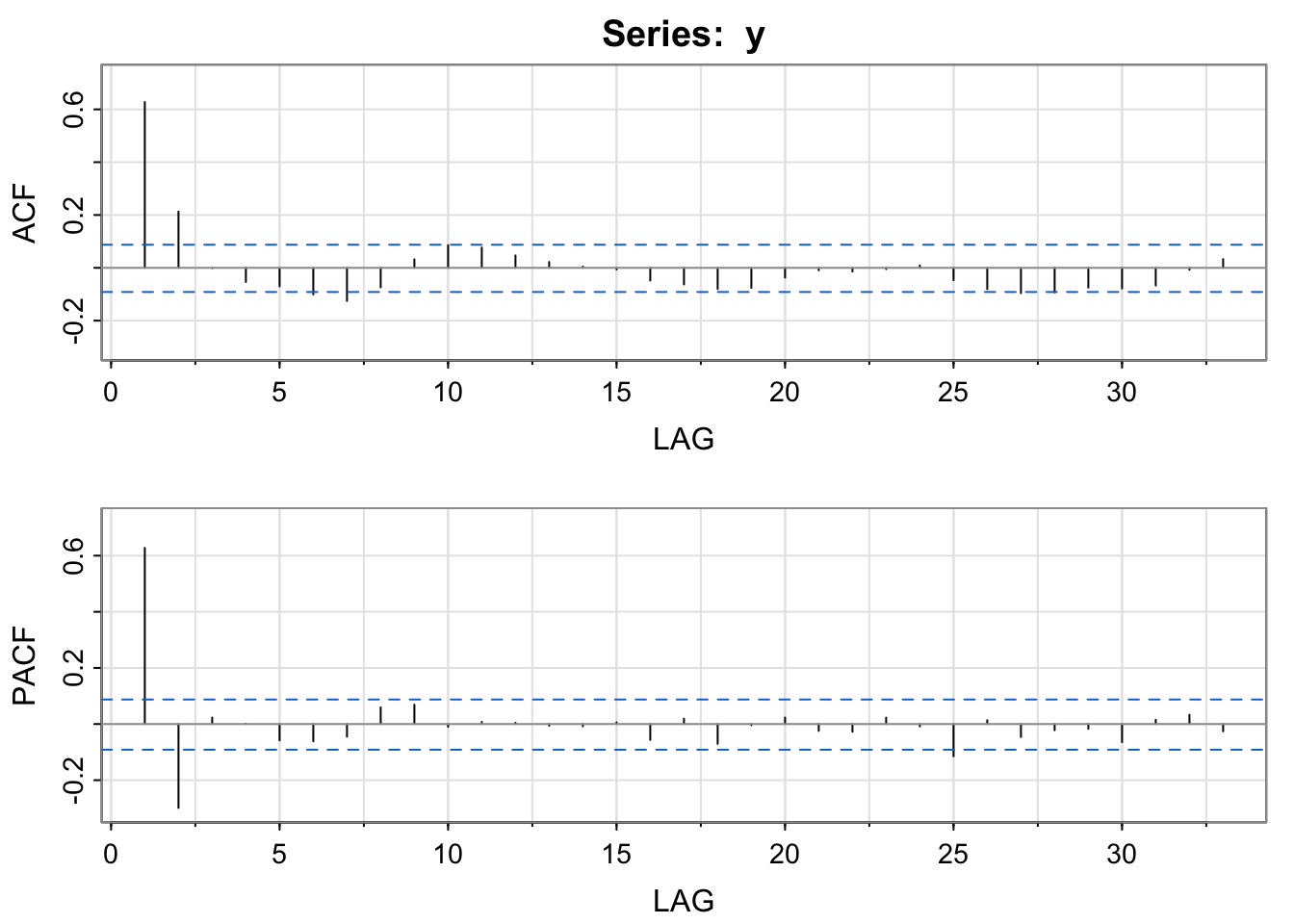
Once you’ve removed trend and seasonality,

  1. Look at ACF and PACF to come up with list of candidate models
  • Use theoretical patterns to help create this list
  1. Fit all candidate models with sarima(data, p, d, q)
  2. Compare models using model selection tools
  • BIC (Bayesian Information Criterion) = - (Goodness of Fit Measure) + penalty [Smaller the better]
  • Hypothesis tests for estimated coefficients
  • Residual plots from sarima() - want high p-values for Ljung-Box and ACF that looks like independent noise

. . .

Example

astsa::acf2(y)

Candidate List: AR(1), AR(2), MA(2)

# Fit all models - Check out Diagnostic plots
mod_ar1 <- sarima(y, p = 1, d = 0, q = 0)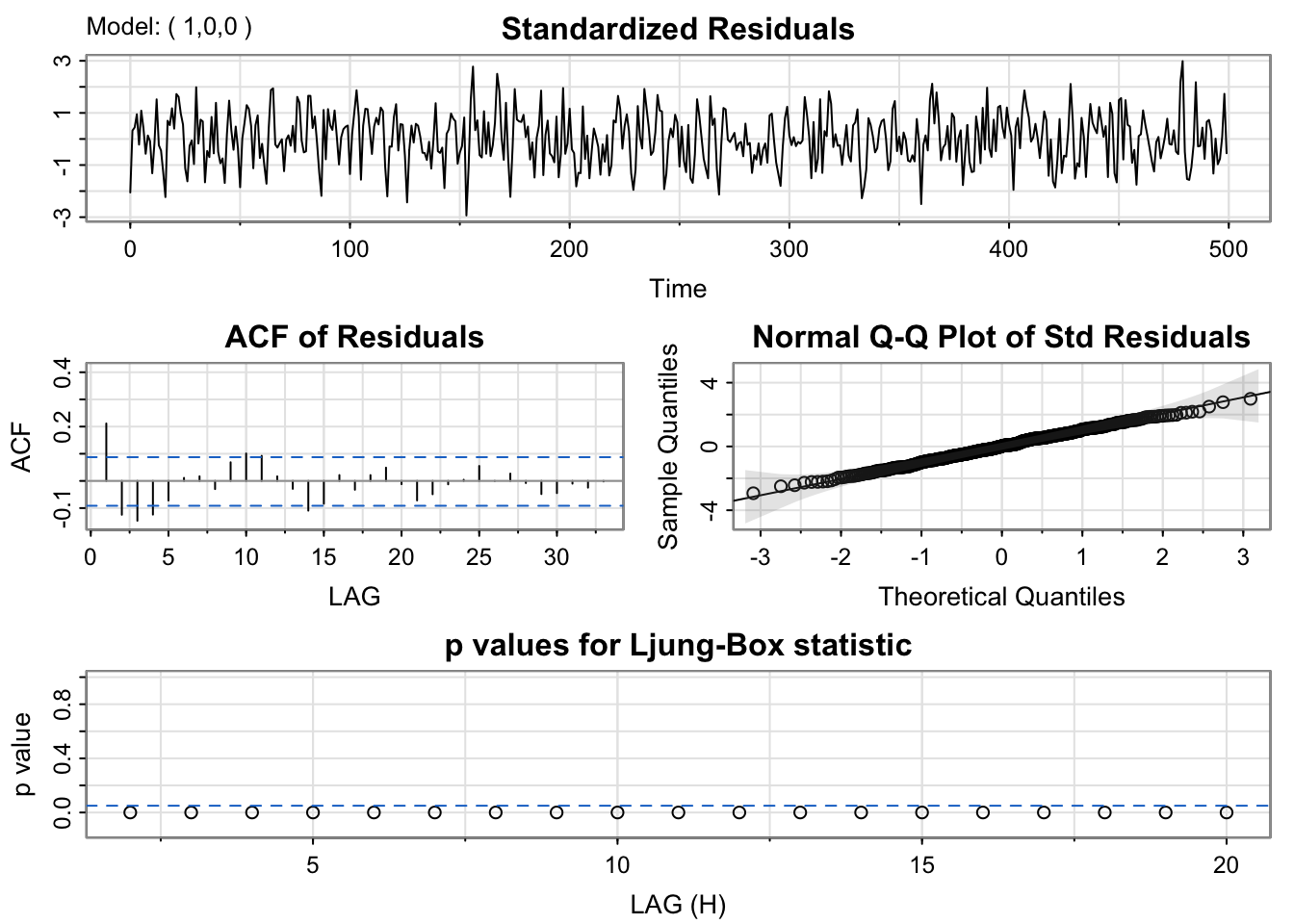

mod_ar2 <- sarima(y, p = 2, d = 0, q = 0)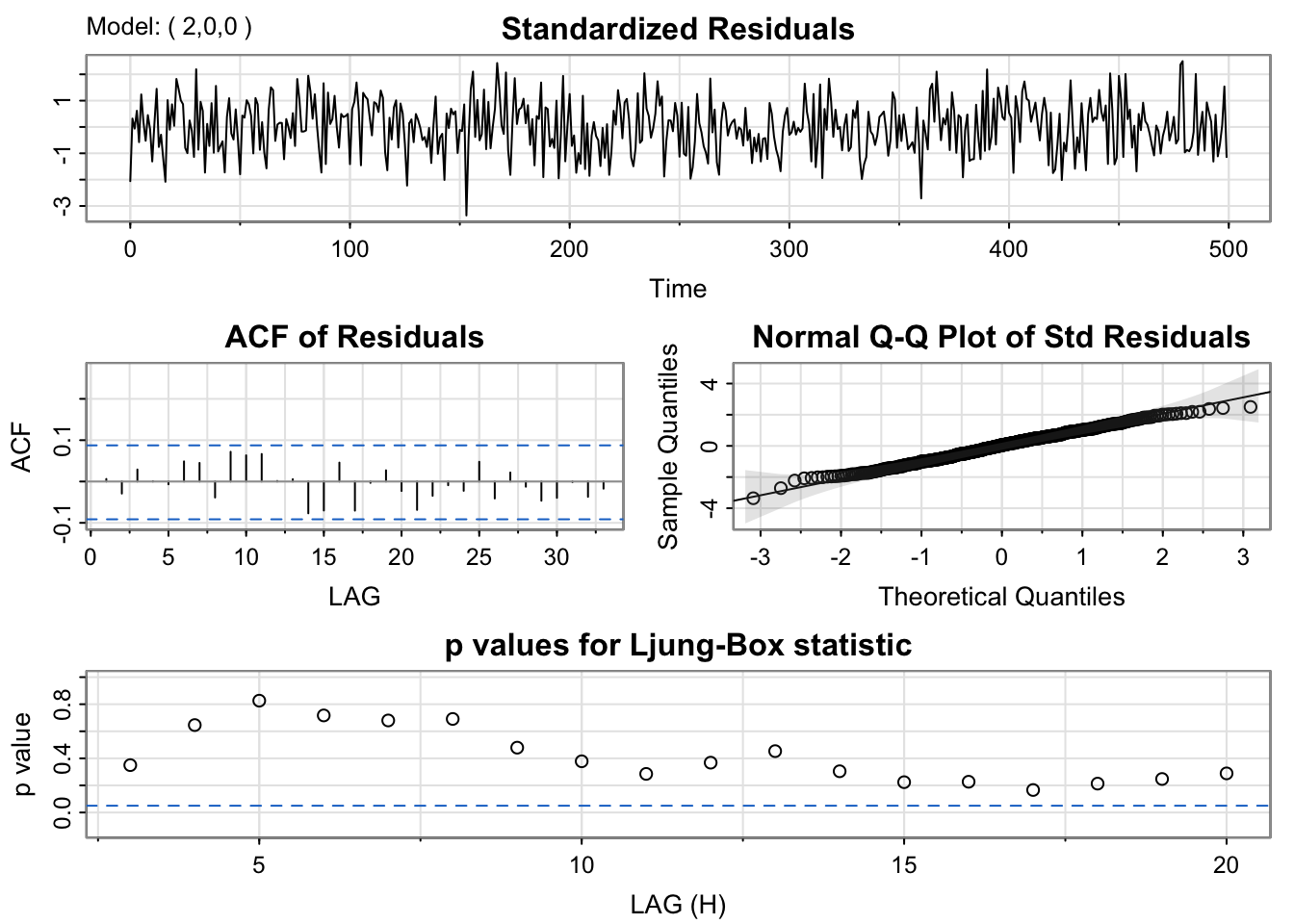

mod_ma2 <- sarima(y, p = 0, d = 0, q = 2)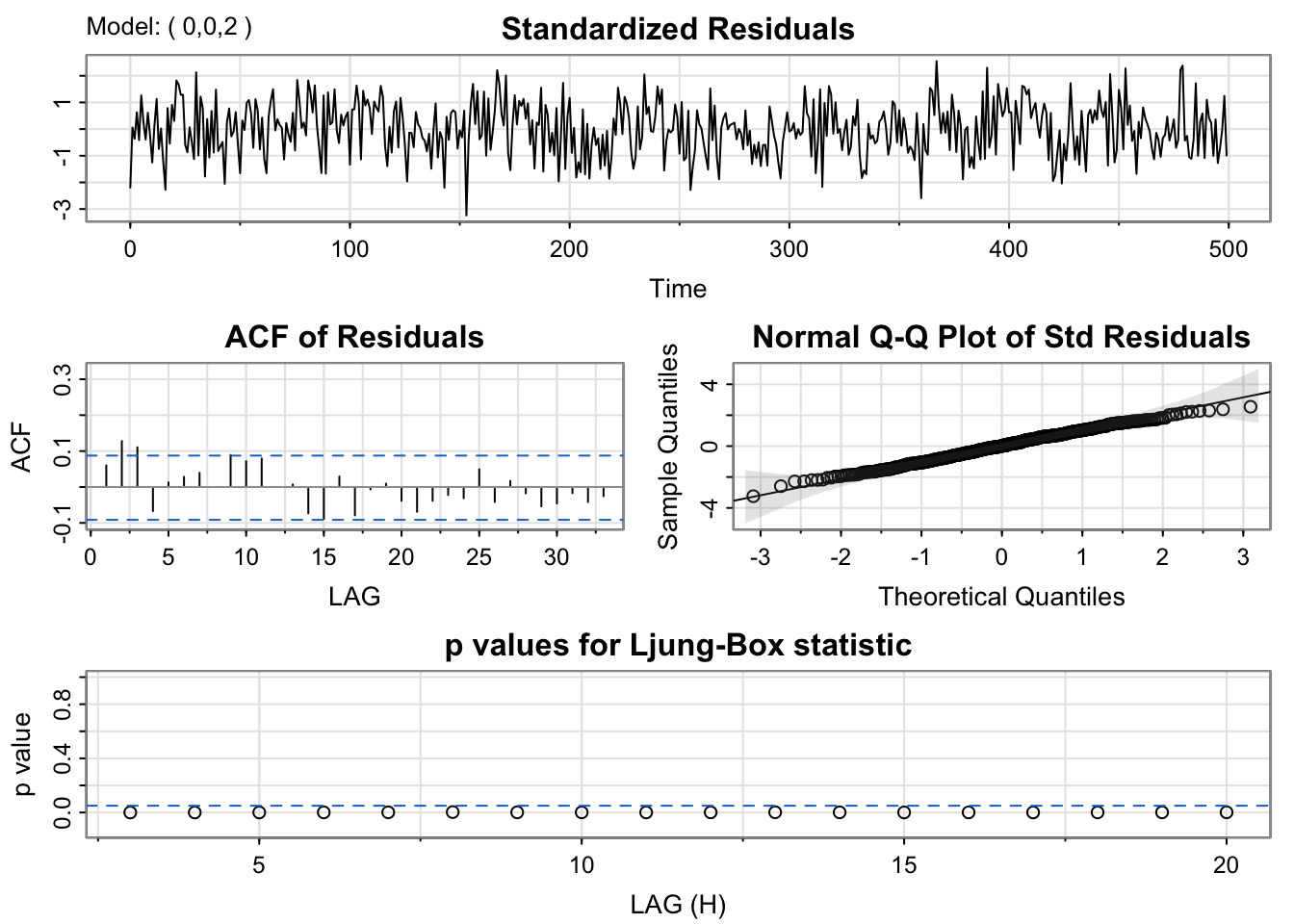

# Check H0: phi = 0
mod_ar1$ttable
      Estimate     SE t.value p.value
ar1     0.7208 0.0311 23.1857  0.0000
xmean   0.0540 0.1754  0.3080  0.7582
mod_ar2$ttable
      Estimate     SE t.value p.value
ar1     0.9378 0.0427 21.9670  0.0000
ar2    -0.3022 0.0428 -7.0666  0.0000
xmean   0.0608 0.1286  0.4728  0.6366
mod_ma2$ttable
      Estimate     SE t.value p.value
ma1     0.8966 0.0399 22.4968  0.0000
ma2     0.3722 0.0374  9.9620  0.0000
xmean   0.0630 0.1084  0.5817  0.5611
# Check BIC, AIC (lower is better)
mod_ar1$ICs
     AIC     AICc      BIC 
3.043172 3.043220 3.068459 
mod_ar2$ICs
     AIC     AICc      BIC 
2.952012 2.952109 2.985729 
mod_ma2$ICs
     AIC     AICc      BIC 
2.990376 2.990473 3.024093

Learning Goals

  • Explain and illustrate how first and second order differences remove linear and quadratic trends.
  • Explain and illustrate how seasonal differences remove seasonality.
  • Fit ARIMA and SARIMA models to real data and use model selection tools to decide on a final model.
  • Explain and illustrate the general theoretical procedure for doing forecasting.


Notes: ARIMA and SARIMA Models

9.1

One Final Model to Rule them All!

Incorporate Trend and Seasonality into the Model

Parametric Model: If we estimate the trend and seasonality using lm() [e.g. polynomials, splines, indicator variables, sine/cosine curves]

  • We can combine that “linear” model with the Noise Model [AR, MA, ARMA] using sarima(xreg = X) where X <- model.matrix(lm(y ~ x, data )) .

. . .


But what does model.matrix() do? or

  • Categorical X variables are converted to indicator variables
  • Spline transformations of X’s are converted to the new complex variables (basis)
  • Interaction terms create products of the X variables

model.matrix(lm(y ~ x, data)) or model.matrix(~ x, data)

. . .


Differencing:

If we use differencing to remove trend and seasonality,

  • We can combine the differencing preprocessing steps with the Noise Model [AR, MA, ARMA] using sarima(d, D, S) where d is the order of lag = 1 differences to remove trend, D is the order of lag = S differences to remove seasonality.

But why do we need one final model?

. . .


Simultaneous Estimation of All Components

Once we’ve made choices for each model component, it is useful to simultaneously estimate one final model

  • To estimate standard errors appropriately
  • To forecast into the future

BUT, what if the residuals from your Noise Model don’t look like independent noise?

Backshift Operators

It can be useful to use the backshift operator, \(B\), to simplify the notation of our models, such that

\[B^k Y_t = Y_{t-k}\text{ for }k = 0,1,2,3,4,...\]

Our \(AR(p)\) can be written as

\[(1 - \phi_1B - \cdots-\phi_pB^p)Y_t = W_t\]

Our \(MA(q)\) can be written as

\[Y_t = (1 + \theta_1B + \cdots+\theta_qB^q)W_t\]

. . .



We can use the backshift operator to simplify the notation for differences.

  • A first order difference to remove a linear trend can be written as

\[Y_t - Y_{t-1} = (1-B)Y_t\]

  • A second order difference to remove a quadratic trend can be written as

\[(Y_t - Y_{t-1}) - (Y_{t-1} - Y_{t-2}) = (1-B)^2Y_t\]

  • A first order seasonal difference to remove seasonality can be written as

\[Y_t - Y_{t-S} = (1-B^S)Y_t\]

  • A combination of first order for trend and seasonality can be written as

\[(1-B)(1-B^S)Y_t = (1 - B - B^{S} + B^{S+1}) Y_t = (Y_t - Y_{t-1}) - ( Y_{t-S}-Y_{t-S-1}) \]

Seasonal ARMA

Why a new model?

If you have removed seasonality (as best as you can) and fit the best possible ARMA model you can…

But if you see a strong seasonal pattern in the residuals (after the ARMA Model),

SOLUTION: You could try to incorporate a Seasonal AR or MA component.

  • This is a way to account for autocorrelation that continues to persist at lags = S, 2S, 3S, etc.

. . .



Definitions:

A Seasonal \(AR(P)\) can be written as

\[(1 - \Phi_1B^S - \cdots-\Phi_PB^{PS})Y_t = W_t\]

A Seasonal \(MA(Q)\) can be written as

\[Y_t = (1 + \Theta_1B^S + \cdots+\Theta_QB^{QS})W_t\]

All together, an \(ARMA(p,q)\) + Seasonal \(ARMA(P,Q)\)

\[(1 - \Phi_1B^S - \cdots-\Phi_PB^{PS})(1 - \phi_1B - \cdots-\phi_pB^p)Y_t \] \[ = (1 + \Theta_1B^S + \cdots+\Theta_QB^{QS})(1 + \theta_1B + \cdots+\theta_qB^q)W_t\]

. . .



Seasonal ARMA Model Selection

To determine the order of a seasonal ARMA, look for patterns on \(j*S\) lags.

Seasonal \(AR(P)\):

  • ACF decays along lags S, 2S, 3S,...;
  • PACF drops after lag = PS along lags S, 2S, 3S, ...

Seasonal \(MA(Q)\):

  • ACF drops after lag = QS along lags S, 2S, 3S,...;
  • PACF decays along lags S, 2S, 3S,...

. . .



Implementation

To fit a SARIMA model, add order P and Q into the \(ARMA(p,q)\) model with

sarima(p,d,q,P,D,Q,S)

Notes: Forecasting

Forecasting is one form of extrapolating to make predictions for the future (unobserved values of the random process).

To forecast, we need to consider predicting the trend, seasonality, and the noise

\[\hat{y}_{t+1} = \underbrace{\hat{f}(t+1|y_1,...,y_{t})}_{trend} + \underbrace{\hat{S}(t+1|y_1,...,y_t)}_{seasonality} + \underbrace{\hat{e}_{t+1}}_{noise}\]

Forecasting Trend

There is no one “best” way to forecast the trend of a time series.

  • It is best to consider a variety of scenerios based on a set of assumptions about the future.

Some Approaches

  • Naive: Predicted trend = the last observed value of the process or last predicted trend value
  • Exponential Smoothing: Predicted trend = weighted average of all past values (weights decays exponentially)
  • Trend Curve: Predicted trend = predicted value from a linear model [with polynomials, splines, etc.]

. . .

What assumptions do you make for each of these approaches?

Forecasting Seasonality

There is no one “best” way to forecast the trend of a time series.

  • It is best to consider a variety of scenerios based on a set of assumptions about the future.

Some Approaches

  • Seasonal Naive: Predicted seasonality = last observed value from same season

  • Seasonal Curve: Predicted seasonality = predicted value from a linear model [with indicator variables or sine/cosine curves]

. . .



What assumptions do you make for each of these approaches?

Forecasting Noise

Some Approaches

  • Naive: If noise has mean 0, predict noise is 0.

  • ARMA Model: Prediction = predicted value using parameter estimates, observed data and residuals

  • ARIMA: Prediction = predicted value using parameter estimates, observed data and their differences

Forecasting using one final model

Implementation

In R: we can use our one final model to forecast into the future using the astsa::sarima.for() function.

astsa::sarima.for(orig_data, p, d, q, P, D, Q, S, xreg, newxreg, n.ahead)
  • SARIMA Inputs: p, d, q, P, D, Q, S
  • Trend/Seasonal Regression Inputs: xreg, newxreg
  • How many predictions to make in the future: n.ahead

Note:

  • To create newxreg, you must create a variable with dates in future.
newdat <- data.frame(date = max(data$date) %m+% months(1:24)) %>% # extend out 24 months
mutate(dec_date = decimal_date(date), month = month(date)) # create date/time variables used in models
  • Then use model.matrix to create a matrix used in model formula to pass to sarima.for.
NewX <- model.matrix(formula, data = newdat)[, -1] # -1 removes intercept column
  • If you use splines, you’ll need to expand the upper boundary knots in the formulas for xreg and newxreg:
formula <- y ~ bs(dec_date, Boundary.knots = c(min(dec_date), max(dec_date) + n.ahead/12 ) #example for monthly data

More Time Series References

Small Group Activity

Download a template Qmd file to start from here.

Simulate the SARIMA Model

Below, there is three R code chunks to generate three time series and show the theoretical and estimated ACF.

  1. For each, write out the data generation model in random process notation like above (using \(\phi\)’s and \(\theta\)’s).
  2. For each, compare and contrast the estimated ACF & PACF and the theoretical ACF & PACF.
  3. For each, add R code to fit the data generation model to the data using sarima.
  4. For each, add R code to forecast into the future 6 time units using sarima.for.

Model 1:

\[Y_t = \]

library(dplyr)
library(astsa)

y1 <- sarima.sim(ar = c(0.9, -0.1))
plot(y1, type='l')

#estimated ACF and PACF
acf2(y1)

#theoretical ACF and PACF
ARMAacf(ar = c(0.9, -0.1),lag.max = 20) %>% plot(type='h',ylim=c(-1,1))

ARMAacf(ar = c(0.9, -0.1), pacf = TRUE,lag.max = 20) %>% plot(type='h',ylim=c(-1,1))

#fit model to data


#forecast

Model 2:

\[Y_t = \]

y2 <- sarima.sim(ma = c(0.7), d = 1, D = 1, S = 6)
plot(y2, type='l')

#estimated ACF and PACF
y2 %>% diff(lag = 1) %>% diff(lag = 6) %>% acf2()

#theoretical ACF and PACF
ARMAacf(ma = 0.7, lag.max = 20) %>% plot(type='h',ylim=c(-1,1))
ARMAacf(ma = 0.7, pacf=TRUE,lag.max = 20) %>% plot(type='h',ylim=c(-1,1))

#fit model to data


#forecast

Model 3:

\[Y_t = \]

y3 <- sarima.sim(ar = c(0.9), sar = 0.5, S = 12)
plot(y3, type='l')

#estimated ACF and PACF
acf2(y3)

#theoretical ACF and PACF
ARMAacf(ar = c(0.9, rep(0, 10), 0.5, -0.9*0.5)) %>% plot(type='h',ylim=c(-1,1))

ARMAacf(ar = c(0.9, rep(0, 10), 0.5, -0.9*0.5), pacf=TRUE) %>% plot(type='h',ylim=c(-1,1))

#fit model to data


#forecast

Summarize your new understanding of SARIMA models and how the SARIMA is different/similar to ARMA models.

Solutions

Small Group Activity

Model 1

Solution

AR(2)

\[Y_t = \phi_1Y_{t-1} +\phi_2 Y_{t-2} + W_t\] \[(1 - \phi_1B - \phi_2B^2)Y_t = W_t\]

library(dplyr)
library(astsa)

y1 <- sarima.sim(ar = c(0.9, -0.1))
plot(y1, type='l')

#estimated ACF and PACF
acf2(y1)

#theoretical ACF and PACF
ARMAacf(ar = c(0.9, -0.1),lag.max = 20) %>% plot(type='h',ylim=c(-1,1))
ARMAacf(ar = c(0.9, -0.1), pacf=TRUE,lag.max = 20) %>% plot(type='h',ylim=c(-1,1))

#fit model to data
fit.mod1 <- sarima(y1,p = 2,d = 0, q = 0)
fit.mod1

#forecast
sarima.for(y1,p = 2,d = 0, q = 0, n.ahead = 6 )

Model 2

Solution

MA(1) + Differencing

\[(1-B^6)(1-B)Y_t = (1 +\theta_1B) W_t\]

\[(1-B^6 - B+B^7)Y_t = (1 +\theta_1B) W_t\]

y2 <- sarima.sim(ma = c(0.7), d = 1, D = 1, S = 6)
plot(y2, type='l')

#estimated ACF and PACF
y2 %>% diff(lag = 1) %>% diff(lag = 6) %>% acf2()

#theoretical ACF and PACF
ARMAacf(ma = 0.7, lag.max = 20) %>% plot(type='h',ylim=c(-1,1))
ARMAacf(ma = 0.7, pacf=TRUE,lag.max = 20) %>% plot(type='h',ylim=c(-1,1))

#fit model to data
fit.mod2 <- sarima(y2, p = 0, d = 1, q = 1, D = 1, S = 6)
fit.mod2

#forecast
sarima.for(y2, p = 0, d = 1, q = 1, D = 1, S = 6, n.ahead = 6 )

Model 3

Solution

AR(1) + Seasonal AR(1)

\[(1-\Phi_1B^{12})(1-\phi_1B)Y_t = W_t\]

\[(1-\Phi_1B^{12} - \phi_1B+\phi_1\Phi_1B^{13})Y_t = W_t\]

y3 <- sarima.sim(ar = c(0.9), sar = 0.5, S = 12)
plot(y3, type='l')

#estimated ACF and PACF
acf2(y3)

#theoretical ACF and PACF
ARMAacf(ar = c(0.9, rep(0, 10), 0.5, -0.9*0.5)) %>% plot(type='h',ylim=c(-1,1))
ARMAacf(ar = c(0.9, rep(0, 10), 0.5, -0.9*0.5), pacf=TRUE) %>% plot(type='h',ylim=c(-1,1))

#fit model to data
fit.mod3 <- sarima(y3, p = 1, d = 0, q = 0, P = 1, D = 0, S = 12)
fit.mod3

#forecast
sarima.for(y3, p = 1, d = 0, q = 0, P = 1, D = 0, S = 12, n.ahead = 6 )

Wrap-Up

Finishing the Activity

  • If you didn’t finish the activity, no problem! Be sure to complete the activity outside of class, review the solutions in the online manual, and ask any questions on Slack or in office hours.
  • Re-organize and review your notes to help deepen your understanding, solidify your learning, and make homework go more smoothly!

After Class

Before the next class, please do the following:

  • Take a look at the Schedule page to see how to prepare for the next class.